Sequential Design of experiments
Published:
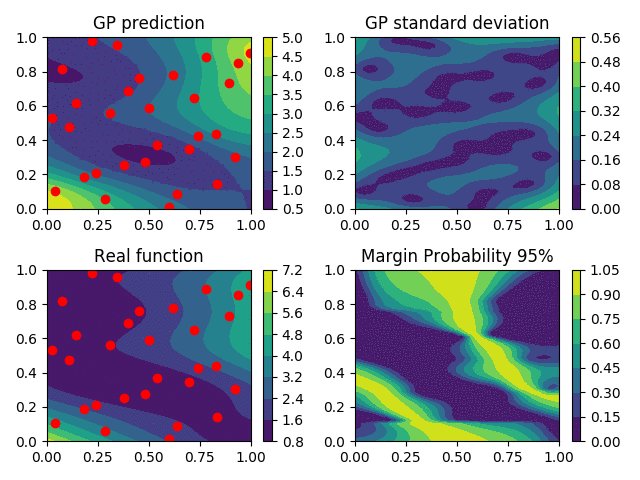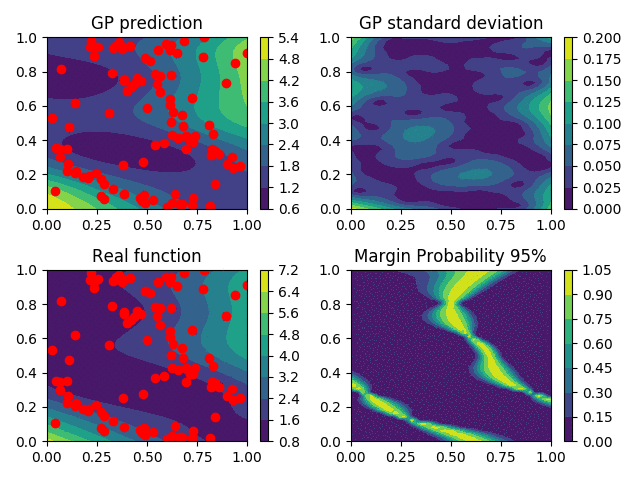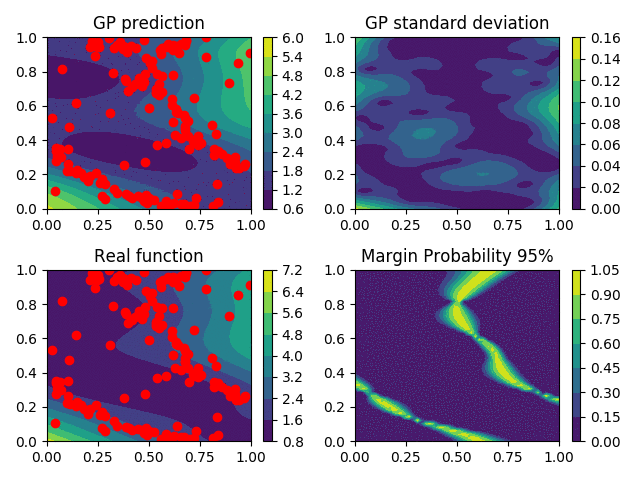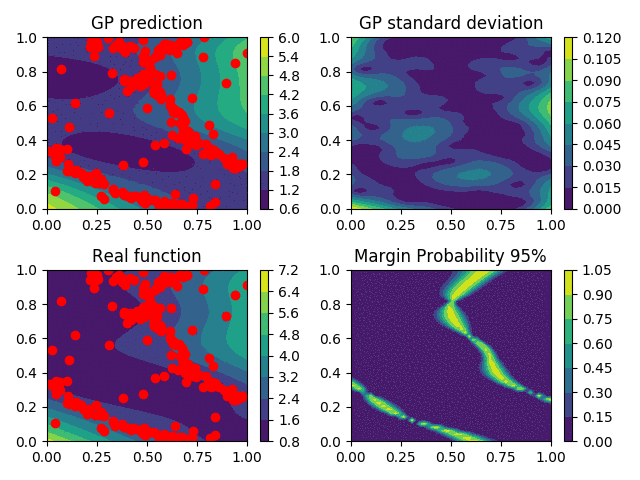
In this post, I will try to present a few methods for sequential design of experiments implemented in a python package. Let us consider that we have a function \begin{equation} f: x\in\mathcal{X} \mapsto f(x) \end{equation}
It can be for instance a quantity computed using expensive simulations. Classically, we can expect that this function has been evaluated on a reasonable initial design, that is for example a space-filling design (LHS, Sobol’ sequence etc)
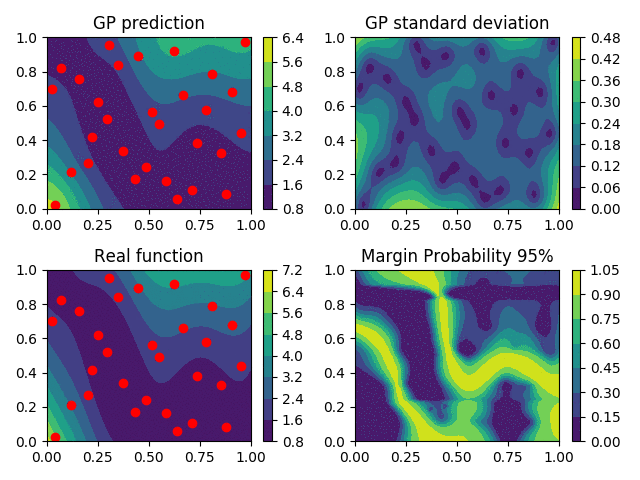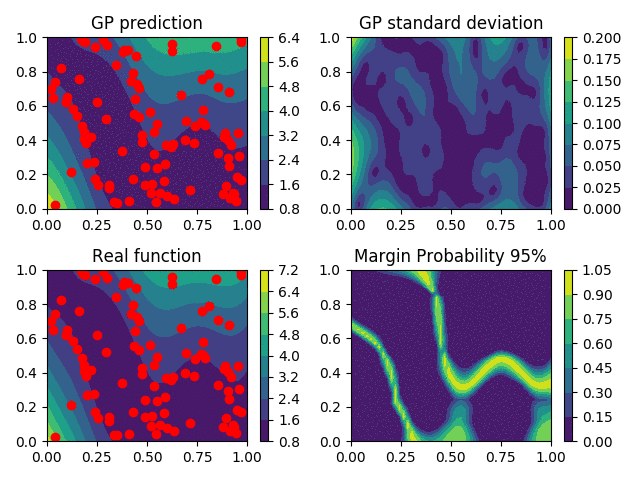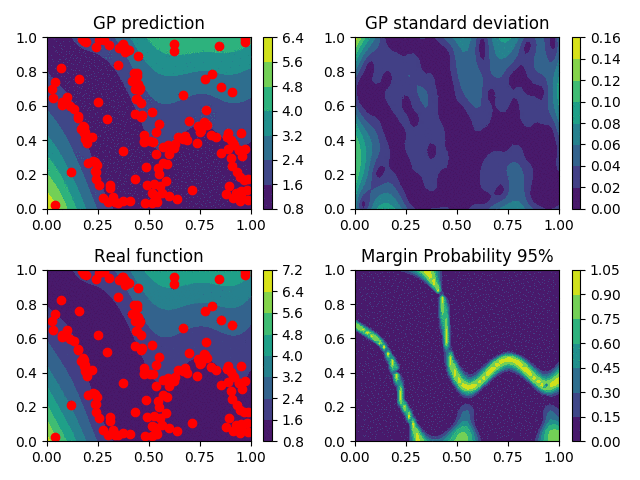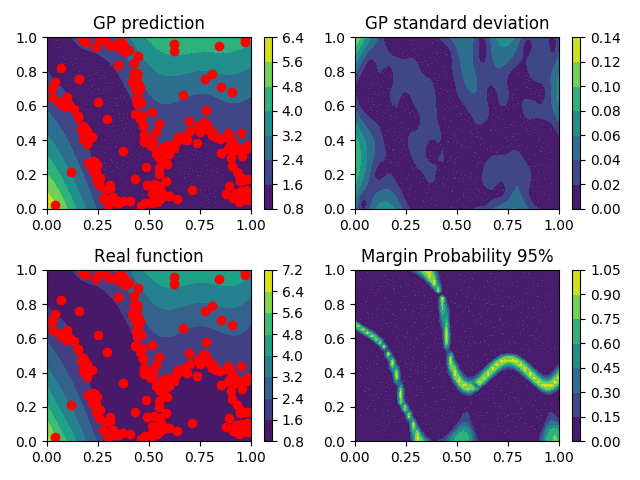
Gaussian Processes as metamodels
One-step look ahead strategies
The main idea is to derive some criterion \(\kappa\), based on the properties of GP, such that its maximiser will be added to the design.
Starting from \(\mathcal{X} = \mathcal{X}_0\), we define \(\mathcal{X}_n\) as \begin{equation} \mathcal{X}_{n-1} \cup \left\{(x_n, f(x_n))\right\} \end{equation}
where \begin{equation} x_{n} = \mathrm{argmax}_{x} \kappa(x, Y) \end{equation}
Sampling based selection strategy
Several strategies exist to extend the one-step strategy presented before to \(q\)-steps strategies, but for them, a increasing computational effort is needed.
Another solution (insert ref) is to use the criterion \(\kappa\) as an unnormalized probability density function, so \(\kappa \propto \pi\) where \(\pi\) is a proper pdf. Using a suited algorithm, samples are generated from \(\pi\), and using a clustering algorithm on those samples, one can select \(q\) points to be evaluated.
This present the advantage that it does not require extensive computations of expectations, that appear in classical \(q\)-steps lookahead strategies. Moreover, it is better suited to deal with the multimodality of the criterion.
Optimisation
Probability of improvement
\begin{equation} \mathrm{PI}(x, Y) = \mathrm{Pr}\left[Y(x) \leq \min_i f(x_i)\right] \end{equation}
Expected-Improvement (EI)
A much more popular choice that leads to the EGO (Efficient Global Optimisation) algorithm is the Expected Improvement \begin{equation} \mathrm{EI}(x, Y) = \mathrm{Ex}\left[\left(\min_i f(x_i) - Y(x)\right)^{+}\right] \end{equation}
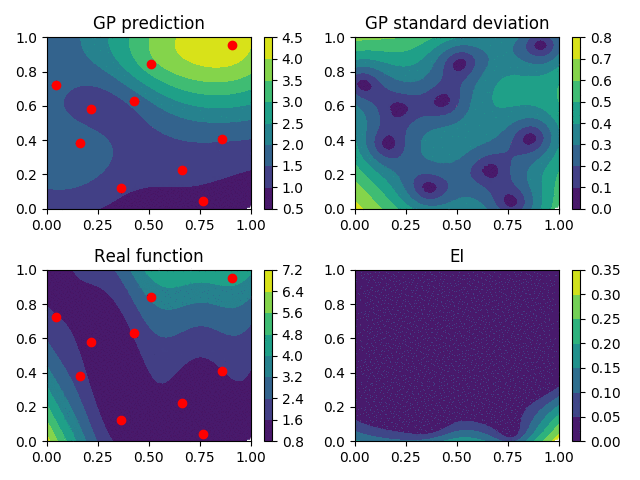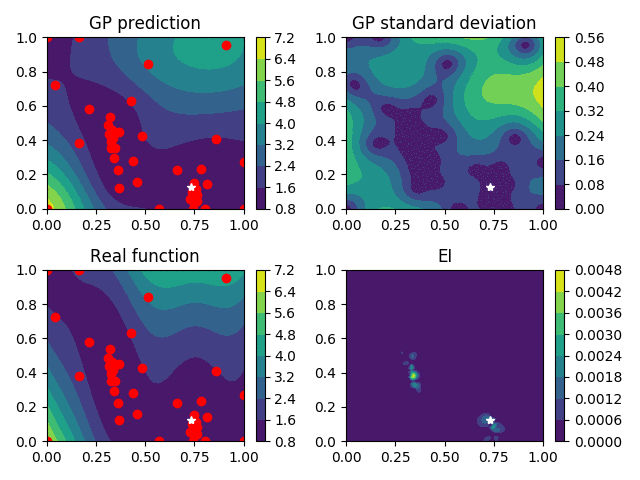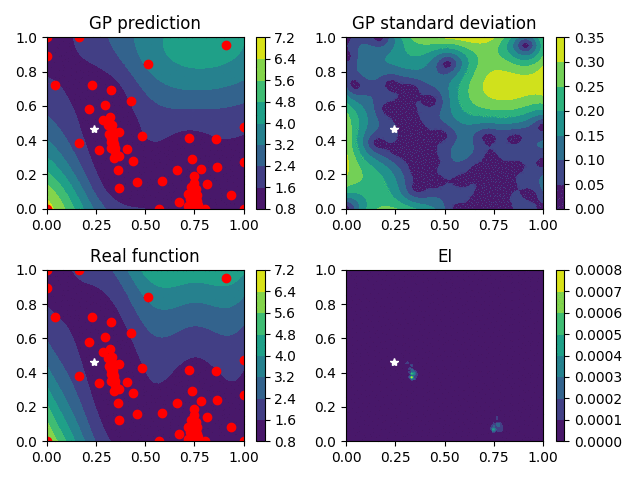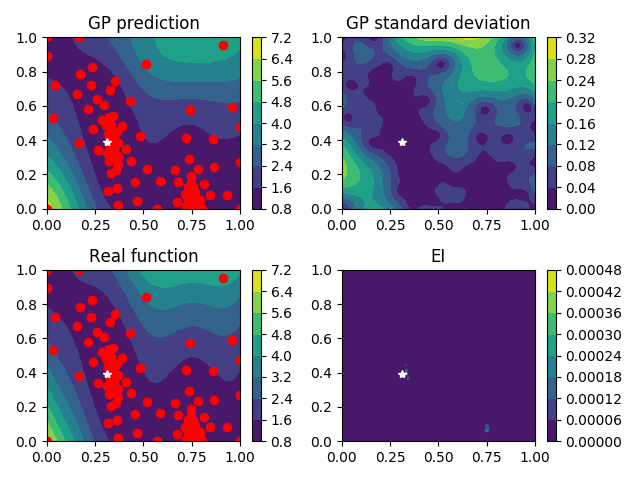
IAGO
Profile Reconstruction
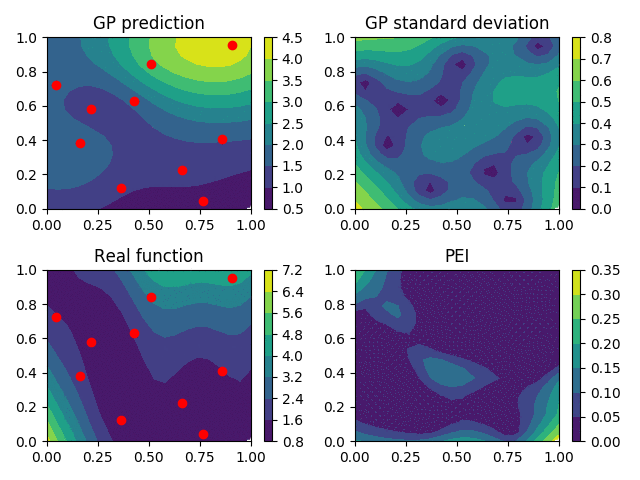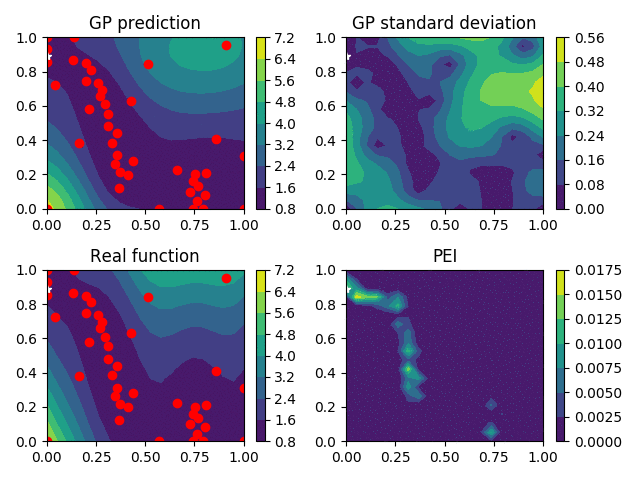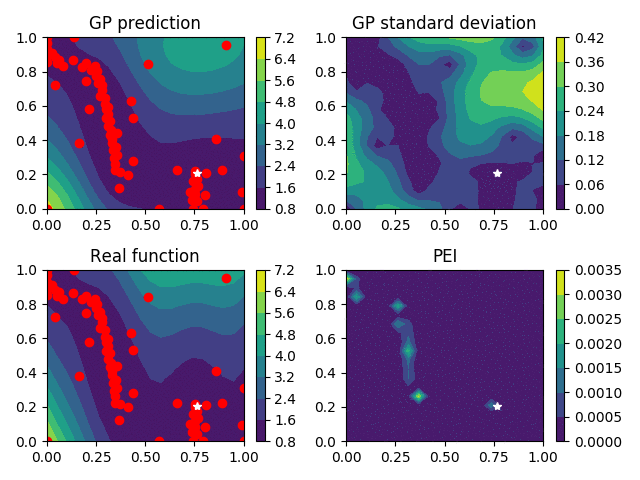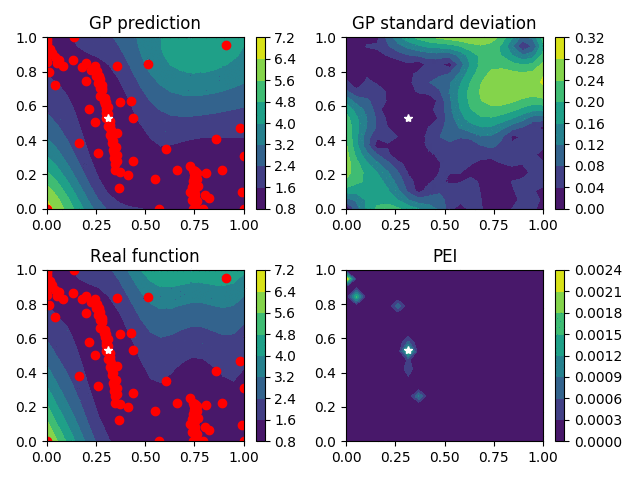
Level-set Reconstruction
Using sample-based strategies
Application to the estimation of \(J(k,u) - \alpha J^*(u)\)